자 이제 frequency spectrum를 이해하기 위해서는 당연히 전 포스트에서의 오일러 공식을 알고 있어야합니다.
이전글(오일러 공식) -> https://hagisilecoding.tistory.com/89
sinusoid
x(t) = Acos(ωt + Φ)
위 식을 이제 어떻게? 바로 오일러 공식으로 표현을 해보겠습니다.
Z = ej(ωt + Φ)
Z* = e-j(ωt + Φ)
코사인만 구하기 위해서는 (Z+Z*)/2를 해주면 됩니다.

일단 X(w) 라는 것은 w에 대한 식을 가르키는 것입니다.
X(w)는 w에 대한 complex amplitude
X(-w)는 -w에 대한 complex amplitude 입니다.
그래서 우리는 sinusoid를 두 개의 complex exponentials로 나타낼 수 있고 이것을 w축을 이용해서 나타내주는 것이 바로 frquency spectrum 이라고 합니다.
하나의 Acos(7t + 0.1) 을 두개의 complex exponentials로 나타내보자.

여기서 특징을 하나 알 수 있는데 w와 -w에 대한 complex amplitude의 관계는 크기는 같고 위상만 반대인 것을 알 수 있다. 이 특징을 conjugate symmetry 라 부른다.
기억해야 할 것!
거의 대부분의 natural signal은 sinusoid 들의 합으로 나타낼 수 있다.
이 말은 즉, 거의 대부분의 natural signal은 2개의 complex exponential 들의 합으로 나타 낼 수 있다.
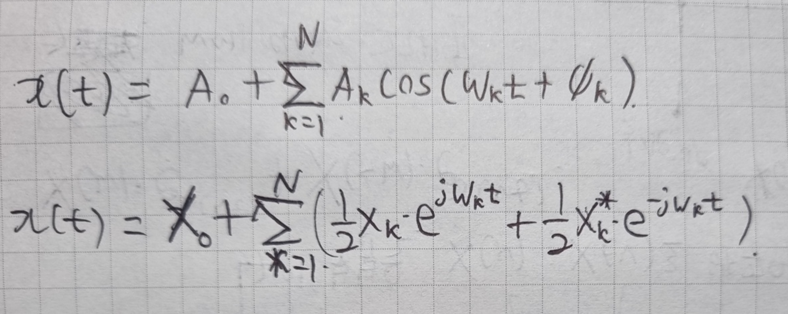
이것을 이해했다면 analysis 와 synthesis도 이해하기 쉽다.
어떤 신호가 있을 때 이 신호는 이제 코사인의 합(sinusoid의 합)으로 나타낼 수 있다.
이것을 분석하면 이제 우리는 frequency spectrum을 알 수 있다.

여기서 위에서는 f에 대한 complex amplitude를 구해주었다.
맨 처음 포스트에 보면 w = 2πf 라는 것을 알 수 있는데 잘 모르겠다면 푸리에 변환 이해하기 첫 번째 포스트로 가면 나와있다.
다음글 CTFS(continuous - Time Fourier seres) ->https://hagisilecoding.tistory.com/91
'CS > 영상처리' 카테고리의 다른 글
| [푸리에 변환 이해하기 - 6] Continuous Fourier Transform (CTFT) [컴공과고씨] (1) | 2022.05.28 |
|---|---|
| [푸리에 변환 이해하기 - 5] Continuous-Time Fourier Series(CTFS 푸리에 급수) (0) | 2022.05.26 |
| [푸리에 변환 이해하기 - 3] Euler's Identity (오일러 공식) (0) | 2022.05.25 |
| [푸리에 변환 이해하기 - 2] complex exponentials (복소지수) 복소평면 이해 (1) | 2022.05.25 |
| [푸리에 변환 이해하기 - 1] Sinusoids (정현파) (0) | 2022.05.25 |