이제 드디어 푸리에 변환에 대해 알아보겠습니다.
Continuous Fourier Transform
앞에 continuous이기 때문에 연속된 신호를 frequency domain으로 바꾸어 주는 것을 말합니다.
여기서 앞의 푸리에 급수와 다른 것은 비주기성을 가진 신호를 sinusoids들의 적분한 것으로 나타낸다는 것입니다.
자 그럼 비주기성 신호를 어떻게 만들면 될까요?
원래 신호의 주기를 무한대로 보내는 것입니다. 이것을 그림으로 표현하자면

위와 같은 x(t) 는 T0라는 주기를 가진다고 했을 때 이 T0를 무한대로 보내면 이 신호는 비주기성 함수가 됩니다.
자 그럼 이것을 CTFT를 해주면 어떻게 될까요?
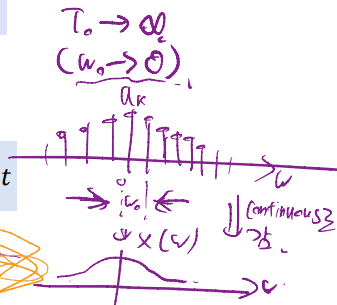
푸리에 급수에서 보았듯이 원래는 discrete하게 신호가 나와야 합니다. 이때 각 ak의 간격을 w0라고 했을 때
위에서 T0를 무한대로 보냈기 때문에 f0(주파수)는 주기의 역수이므로 0으로가고 f= 2πw이기 때문에 w0도 0으로 갑니다.
그림에서 볼 수 있듯이 그래서 ak간격이 0으로 좁아져 결국 x(w)는 연속한 신호를 얻게 됩니다.

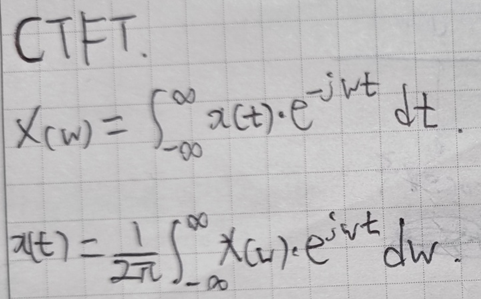
X(w)를 구할때는 일단 연속된 신호에 관한 것이기 때문에 적분을 취해주어야 하구요 또한 w가 남아있어야 하니 t에 관한 적분으로 해주고 주파수로 변환할 때는 보통 시계방향으로 돌게 만들기 위해서 -를 붙어줍니다.
Inverse CTFT도 마찬가지로 X(w)의 신호가 연속이기 때문에 적분을 취해주어야합니다.
앞에 1/2pi를 곱해주는 것은 normalized해주는 것이라고 보면 됩니다. 적분 범위는 T를 무한대로 보냈기 때문에 -∞ 에서 ∞로 해주면 됩니다.
이렇게 생각해주어서 공식을 외워주는게 좋습니다. 뒤에 특징와 여러 푸리에 변환 공식이 나오면 헷갈리기 때문에 이해를 하고 가야 헷갈리지 않습니다.
2D

이건 2D에서의 푸리에 변환 입니다. 이미지를 변환 할 때는 좌표이기 때문에 2D 식을 적용해 주어야 합니다.
1D를 이해하고 있다면 2D도 어렵지 않게 이해하실 수 있을 것 입니다.
다음글 Sampling and Reconstruction -> https://hagisilecoding.tistory.com/93
'CS > 영상처리' 카테고리의 다른 글
| [푸리에 변환 이해하기 - 8] Discrete Time Fourier Transform (DTFT) [컴공과고씨] (0) | 2022.05.29 |
|---|---|
| [푸리에 변환 이해하기 - 7] Sampling & Reconstruction & shannon Sampling Theorem [컴공과고씨] (0) | 2022.05.28 |
| [푸리에 변환 이해하기 - 5] Continuous-Time Fourier Series(CTFS 푸리에 급수) (0) | 2022.05.26 |
| [푸리에 변환 이해하기 - 4] frequency spectrum (주파수 스펙트럼) (1) | 2022.05.25 |
| [푸리에 변환 이해하기 - 3] Euler's Identity (오일러 공식) (0) | 2022.05.25 |