이제 본격적으로 푸리에 변환에 대해서 다루겠습니다.
푸리에 변환는 기본적으로 우리가 time domain에서 다루던 신호를 frequency domain으로 변환하는 것 입니다.
이 말은 우리는 어떤 주파수 성분이 있는지 분석할 수 있고 이것을 토대로 높은 주파수는 뺄 수도 낮은 주파수를 빼거나 등 주파수 성분들을 조작할 수 있게 됩니다.
앞에서 말했듯이 자연 신호는 sinusoid들의 합으로 나타낼 수 있습니다. 또한 이 sinusoids들은 기본 주파수의 배수로 만들 수 있습니다.
Continuous-Time Fourier Series
어떤 주기 함수든 우리는 harmonic frequencise(기본 주파수의 배수)의 sinusoids의 합으로 표현이 가능하다는 것이다.
*기본 주파수의 배수 : wk = kw0
그래서 푸리에 급수는 신호에 e-jkω0t와 내적을 해서 적분해주면 그 주파수에 대한 닮은 정보가 나온다는 것입니다.
여기서 e-jkω0t은 e-jk2πft라고 쓸수 있겠죠? 그럼 이제 익숙한 모양일 것입니다.
바로 회전변환 식 입니다. 만약 신호가 e-jk2π(0.5)t 라고 한다면
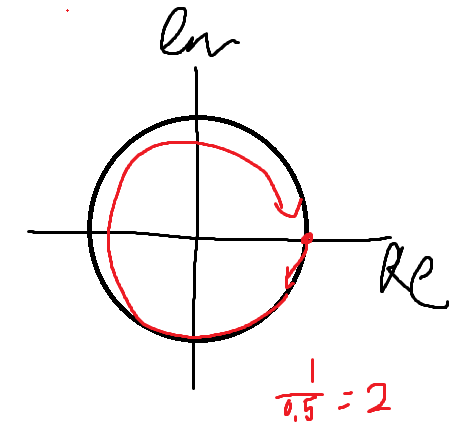
이런 모양으로 2초에 한번 회전하는 회전 함수라는 것을 알 수 있습니다.
여기서 f는 진동수이기 때문에 2πf를 w(각속도)로 바꾸어 줄 수 있습니다. 또한 -라는 회전 방향을 뜻합니다. 기본적 양수이면 반시계로 돌고 음수이면 시계방향으로 돈다는 뜻입니다. 푸리에 변환에서는 기본적으로 시계 방향으로 돌게 하기 위해서 주파수 도메인으로 변환할 때 e-jkω0t를 곱해준다고 생각하면 나중에 공식을 외울때 어느쪽이 음수인지 헷갈리않고 이해할 수 있습니다.
수학에서의 적분은 이제 얼마나 닮은 정보가 있냐라는 것을 의미하기 때문에 우리가 주파수의 배수를 곱해서 더해주면 그 주파수 성분과 우리의 신호가 닮았는지에 정보가 나오게 되고 이 값을 이용하여 우리의 신호를 주파수 성분별로 나누는 것이 푸리에 변환의 큰 틀입니다.
Continuous-Time Fourier Serises (CTFS)
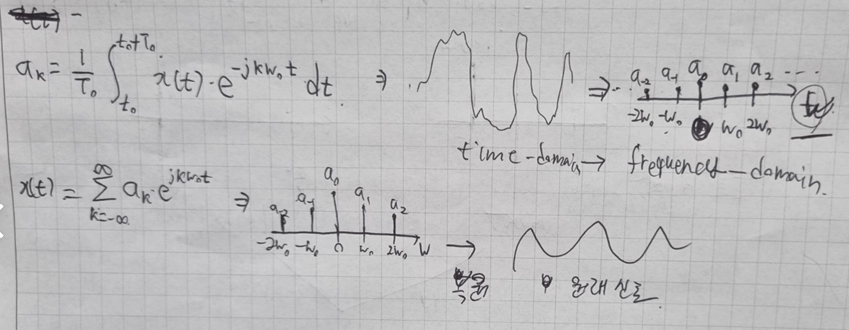
주파수 성분을 구하기 위해서는 e-jkω0t를 곱해주고 다 더해주면 됩니다. x(t)는 연속신호이기 때문에 적분을 취해준 것입니다. 반면 inverse를 할 때는 보시면 ejkω0t를 곱해주고 시그마를 취해주는데 이유는 ak는 이산신호이기 때문에 시그마를 취해준 것이라고 볼 수 있습니다.
다음글 CTFT(Continuous-Time Fourier Transform) -> https://hagisilecoding.tistory.com/92
'CS > 영상처리' 카테고리의 다른 글
| [푸리에 변환 이해하기 - 7] Sampling & Reconstruction & shannon Sampling Theorem [컴공과고씨] (0) | 2022.05.28 |
|---|---|
| [푸리에 변환 이해하기 - 6] Continuous Fourier Transform (CTFT) [컴공과고씨] (1) | 2022.05.28 |
| [푸리에 변환 이해하기 - 4] frequency spectrum (주파수 스펙트럼) (1) | 2022.05.25 |
| [푸리에 변환 이해하기 - 3] Euler's Identity (오일러 공식) (0) | 2022.05.25 |
| [푸리에 변환 이해하기 - 2] complex exponentials (복소지수) 복소평면 이해 (1) | 2022.05.25 |