저번 글에서 기본적이 intensity transformations에서 공부했습니다.
이번에는 histogram equalization에 대해서 알아보겠습니다.
unnormalized histogram

위 그림 처럼 m*n의 픽셀들이 나열되어있을 때 각 픽셀이 나타내는 밝기가 0~n까지 있다면 밝기가 0인 칸의 개수 1인 칸의 개수 쭉쭉 세어서 옆의 그래프 처럼 나타낸 것이다.

히스토그램의 bin을 이용해서 범위를 지정해 그 범위 밝기에 속한 칸의 개수를 세어 그래프를 만들어준 것이다. 이 때 이 범위를 bins라고 합니다.
unnormalized histogram가 있으니 normalized histogram도 있다.
normalized histogram는 unnormalized histogram에서 모든 값이 1이 되어지도록 만들어 준 것이다.
즉, 각 값을 총 픽셀의 개수로 나누어 주면 된다.
p(r) = h(r)/MN 여기서 p(r)의 모든 합은 1.
Histogram Equaliztion
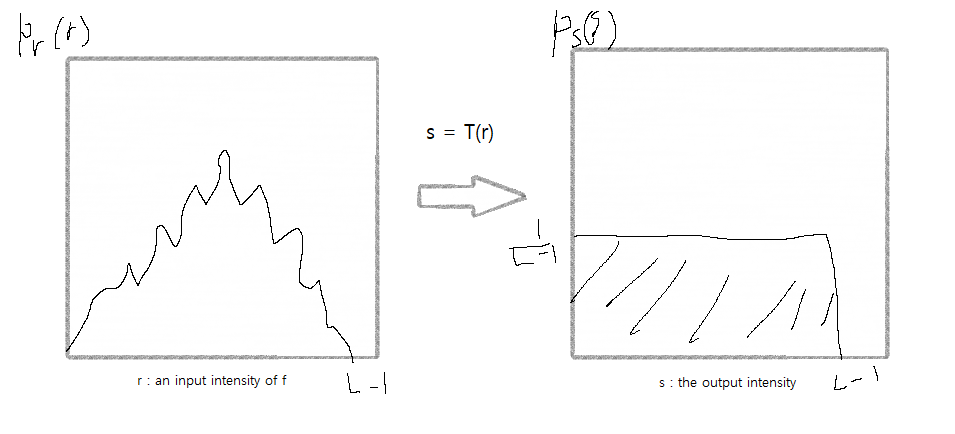
이런식으로 몰려있는 부분을 uniform 분포로 바꾸어 주는 것을 말한다.
여기서 각각의 밝기 값들을 T(r)의 밝기 값으로 바꾸어 주는것인데 중요한 것은 이 T(r) 값은 monotonic increasing이여야 한다. Monotonic increasing은 값은 같아도 되지만 감소해서는 안되는 것을 뜻한다.

그러나 컴퓨터는 discrete 값을 원하기 때문에 contiuous에서 discrete 값으로 변환을 해주어야한다.
그래서 s=round(T(r)) => 반올림을 해주어 discrete하게 만들어 준다.
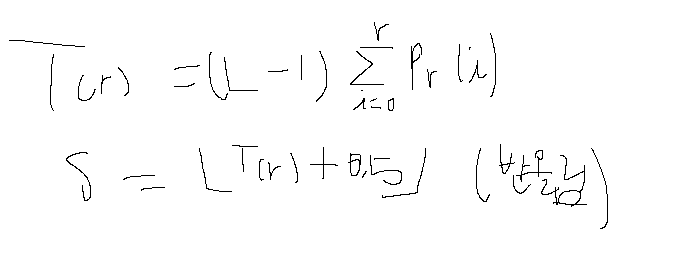
이런식이 나오게 된다.
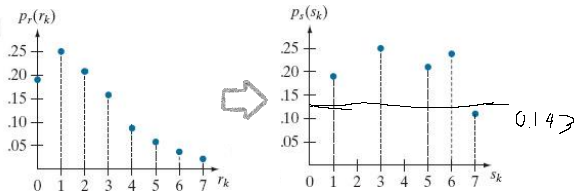
원래는 왼쪽을 히스토그램 평탄화를 해주면 1/7인 0.143이 나와야 하지만 discrete하게 값을 바꿔주기 위해 반올림을 하다 보니 0 과 2는 나오지 않아 전체합을 1로 맞추어 주기위해 어떤 값은 좀 더 크게 어떤 값은 낮게 나오게 됨을 볼 수 있다.
Histogram Matching
이것은 히스토그램 평탄화가 평탄하게 만드는 것이였다면 히스토그램 매칭은 원하는 모양으로 바꾸어 주는 것을 말한다.

원리는 위 그림처럼 원하는 것을 먼저 uniform하게 만들어 그것의 역함수를 구해준다. 그 후 origin을 uniform하게 만든 후 아까 구한 역함수에 origin을 uniform하게 만든 것에 값을 넣어주어 출력해주면 된다. 이렇게 하면 우리가 원하는 히스토그램의 분포를 만들 수 있다.
Local Histogram Statics
이것은 이제 부분적인 곳을 변환할때 쓰는 것인데 예를 들면

지금 보면 가운데에 a가있는데 잘 보이지 않아 global 이퀄라이즈를 했지만 영상이 나아지지 않는 모습이다.
반면 local로 해준다면 전체 픽셀의 평균에 이 아닌 이웃한 픽셀의 평균을 가지고 계산을 해준다.

그래서 이런식으로 글자를 강조할 수 있다.

보면 1번째 조건식(K0 = 0.4 일 때)은 부분적인 평균이 mg를 k0만큼 어둡게 했을 때 보다 밝다면
2번째 조건식(k1 = 0.02, k2=0.4) 검은 쪽의 분산은 거의 0이 될거고 글자의 분산쪽은 0보다는 클것이다 그렇기 때문에 이것을 이용해서 분산이 저 식 사이에 있다면
-> E를 곱하여 강조를 해주는 것이다.
'CS > 영상처리' 카테고리의 다른 글
| [영상처리] Highpass Spatial Filters - Laplacian filter, Unsharp Masking (윤곽선 추출 필터) [컴공과고씨] (1) | 2022.03.30 |
|---|---|
| [영상처리] LowPass Spatial Domain Filter [공간 도메인 필터] [컴공과고씨] (0) | 2022.03.25 |
| [영상처리] LTI 시스템 & Convolution [컴공과고씨] (0) | 2022.03.24 |
| [영상처리] signal 과 systems, LTI systems, impulse response [컴공과고씨] (0) | 2022.03.24 |
| [영상처리] Intensity Transformations(밝기 값 변환)(1) [컴공과고씨] (1) | 2022.03.21 |