오늘은 highpass spatial filters에 대해 볼것이다.
highpass spatial filters는 고주파만 통과시키는 필터이다.
일단 이 필터에 대해 알아보기 위해서는 미분을 이용하는 것에 대해서 살펴봐야 이해를 할 수 있다.
Derivatives & Finite differences
derivatives는 미분값을 이용한 함수로 finite differences(함수값의 차를 이용한 미분계수에 근사시킴)의 용어로 정의가 될 수 있다.
First derivatives of digital function (1차 미분을 이용 -> 기울기)
Second derivatives of digital function (1차 미분을 이용 -> 기울기의 변화량)
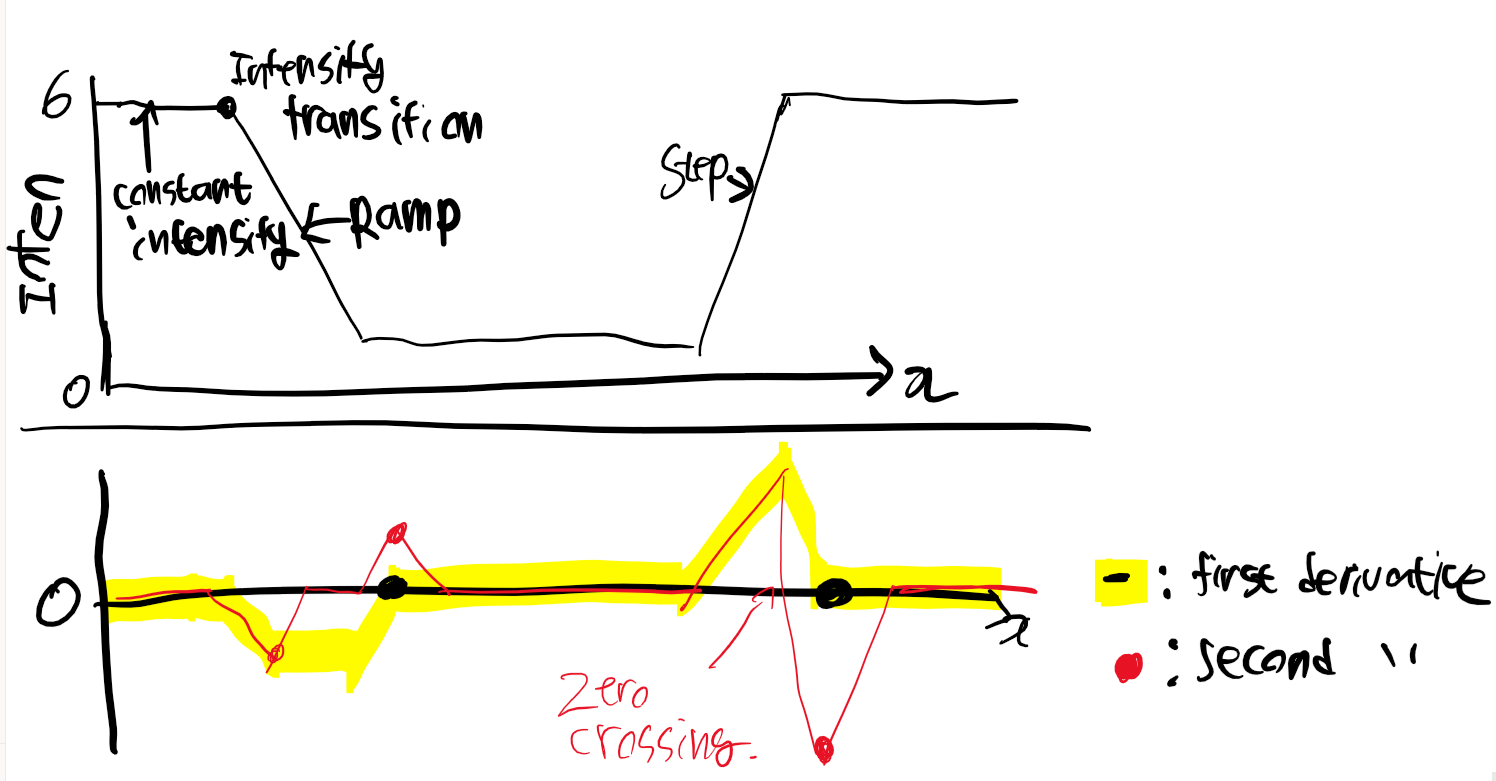
위 그래프를 이용하여서 1차 미분, 2차미분 특징을 알아볼 것이다.
1. 값이 변하지 않는 부분 Constant intensity
-> 1차 미분인 경우 : 값이 변하지 않으므로 기울기 값은 0
-> 2차 미분인 경우 : 기울기의 변화량이 0 이므로 2차 미분 값 0
2. 값이 변하는 부분 Intensity translation
-> 1차 미분인 경우 : 값이 변하여 6에서 5로 즉, 기울기의 값은 -1
-> 2차 미분인 경우 : 기울기의 변화량이 -1 이므로 2차 미분 값 -1
3. 값이 일정하게 변하는 부분 Ramp
-> 1차 미분인 경우 : 값이 일정하게 변하고 있음, 기울기의 값은 -1
-> 2차 미분인 경우 : 기울기의 값은 -1로 일정하기 때문에 2차 미분값은 0
4. 값이 갑자기 확 튀는 부분 Step
-> 1차 미분인 경우 : 값이 확 튀어서 기울기 값이 6까지 올라감
-> 2차 미분인 경우 : 기울기 변화가 0에서 6까지 일어나서 2차 미분값 6
5. Step 구간 다음
-> 1차 미분인 경우 : 그 다음 값들이 일정한 기울기를 가지므로 1차 미분값 0
-> 2차 미분인 경우 : 기울기의 변화량 6에서 0으로 내려간 것이므로 2차 미분값은 -6
즉, 2차 미분인 경우 밝기의 변화가 큰 값에는 + 에서 - 로 가는 Zero crossing이 일어남
이것을 이용하면 우리는 밝기의 변화가 큰 애들을 찾을 수 있음.
미분을 통해 마스크를 만들기

Laplacian Filter(영상의 밝기의 변화율이 큰 녀석을 찾는데에 용이한 필터)
위 미분 법을 이용하여 라플라시안 필터를 만들어 줄 수 있다.

위 식을 이용하여 라플라시안 필터를 만들면

자 그럼 위 필터를 영상에 적용하면 어떻게 될까?
바로 영상의 밝기의 변화가 큰 녀석들만 찾아주게 만드는 것이다.
그러면 우리는 이 것을 가지고 원본영상에 더해서 대비를 더 크게 만들어 줄 수 있게 된다.
이것이 바로 Sharpening이다.
Sharpening(Deblurring)

자 여기서 C에 어느값을 곱하느냐에 따라 경계부분을 더 살릴수도 있다.
라플라시안 마스크를 쓰지 않고도 경계부분을 만들 수 있다.

이런 식으로 원본에서 Blurred 된 영상을 빼주면 unsharp mask를 얻을 수 있다. 이것을 원본에 더해주면 sharpened 된 신호를 얻게 된다.
'CS > 영상처리' 카테고리의 다른 글
| [영상처리] Simple Detectors(Edge, Point, Line) - 경계, 선, 점 검출 [컴공과고씨] (0) | 2022.04.06 |
|---|---|
| [영상처리] Denoising(잡음제거) - (Mean filter, Order-Statistic Filters) [컴공과고씨] (2) | 2022.04.01 |
| [영상처리] LowPass Spatial Domain Filter [공간 도메인 필터] [컴공과고씨] (0) | 2022.03.25 |
| [영상처리] LTI 시스템 & Convolution [컴공과고씨] (0) | 2022.03.24 |
| [영상처리] signal 과 systems, LTI systems, impulse response [컴공과고씨] (0) | 2022.03.24 |