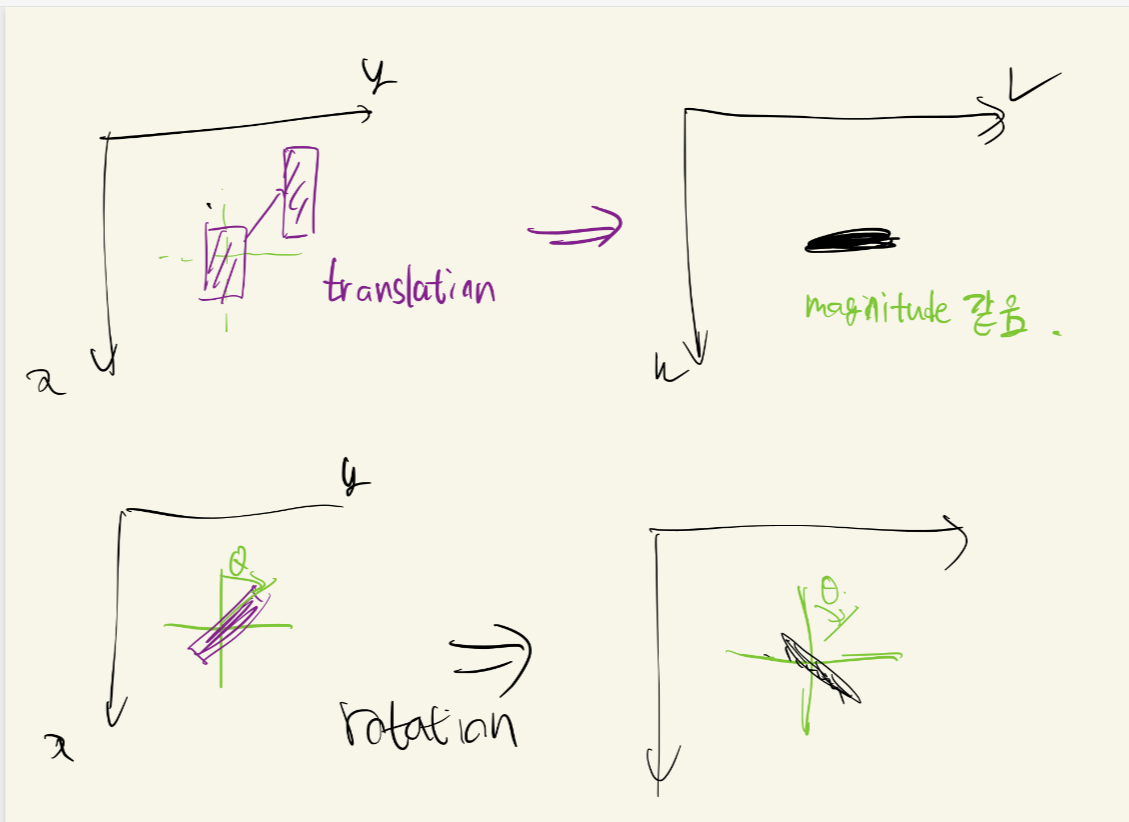
앞에 푸리에 변환에 대해서 깊게 배운 이유는 바로 주파수 도메인에서 이미지에 무언가를 조작하기 위해서 입니다.
그래서 이제는 주파수 도메인 필터링을 공부할 것인데 그전에 디지털 이미지에서의 2-D DFT에 대한 특성들을 이해하고 넘어가려고 합니다. 앞에 푸리에 변환을 잘 이해했다면 비슷비슷해서 이해하기 쉬울 것입니다.
Periodity

2-D DFT의 공식은 1-D하고 거의 비슷하구요
중요한건 주기성을 가진다.
앞에서도 말했듯이 주기반복된 신호를 DFT를 한 것이기 때문에 항상 주기반복 된 결과에서 N - Point를 뽑아 낸 것이기 때문에 N마다 주기반복이 되고 있다고 생각해주어야합니다.
그래서 M과 N을 주기로 하고 있기 때문에 저런 주기성을 가진 특성을 가집니다.
Magnitude & Phase
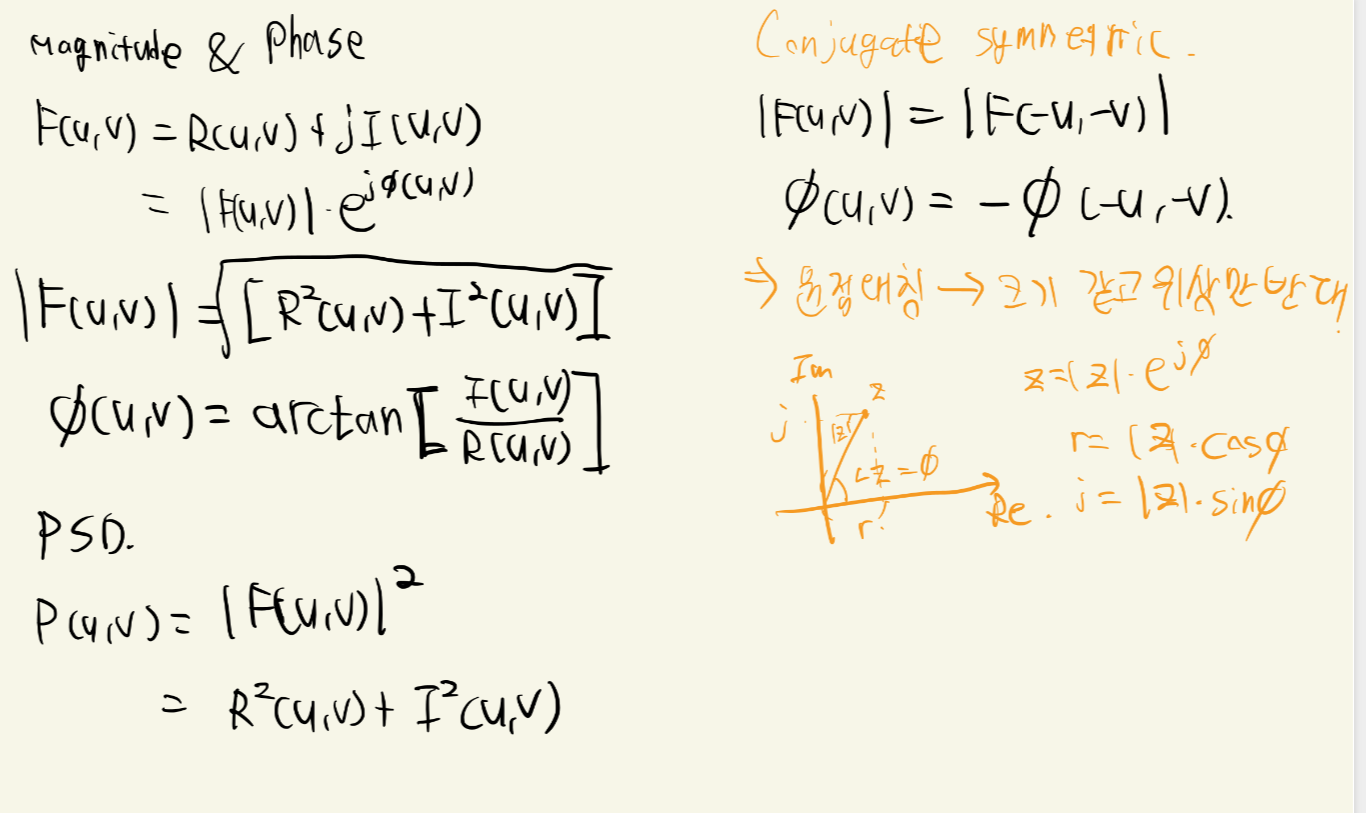
크기는 실수부 + 허수부
위상은 아크탄제트[실수부/허수부]
원점 대칭 -> 크기만 같고 위상만 반대
DC Component

DC라는 건 전류에서 직류를 말합니다. 이것은 한 신호로 쭉 가는 것을 말합니다. 이 뜻은 무엇이냐 sinusoid에서 주파수가 0일 때 sin(φ)가 되므로 sin(φ)로 쭉 가게 됩니다.
그래서 DC가 뜻하는 말은 주파수가 0인 것이기 때문에 주파수를 0으로 놓고 계산을 해주면 signal 를 다 더한 값이 나오게 됩니다.
그래서 평균은 F(0,0)/MN이 됩니다.
Translation & Rotation
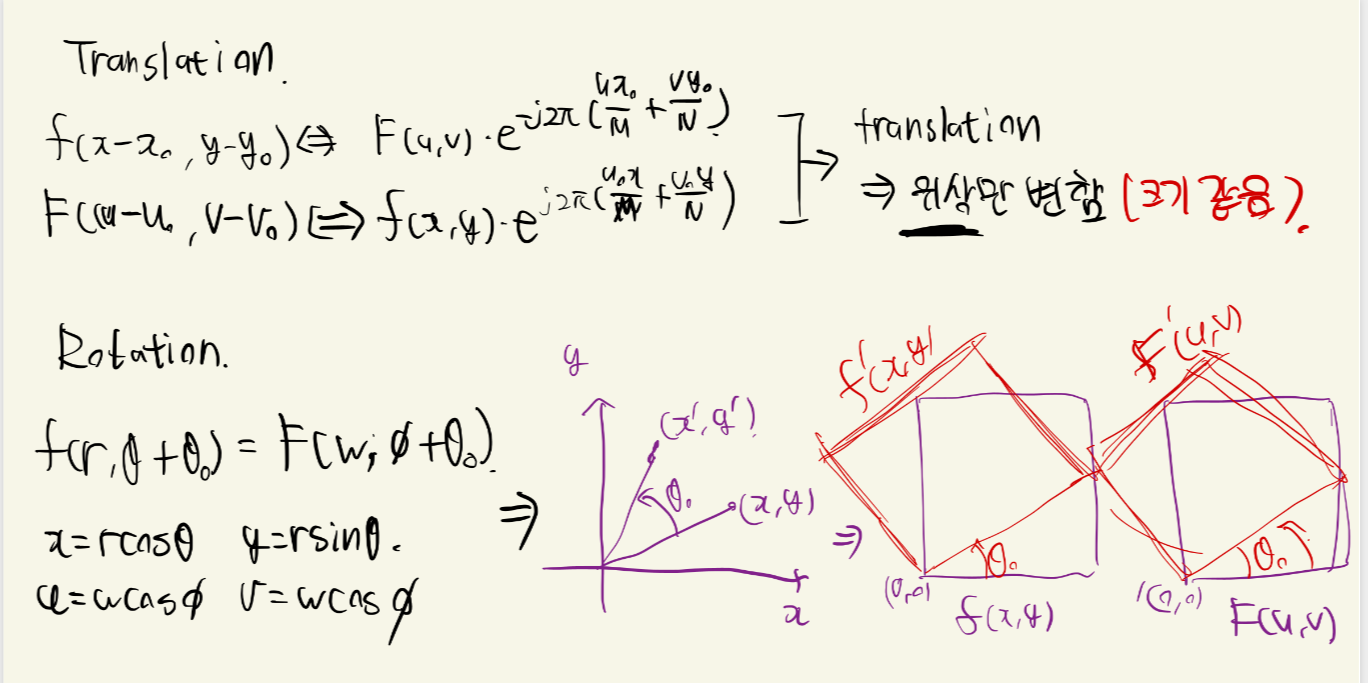
자 이동변환이 되면 다른 도메인에서는 ? 위상만 변하는 것을 알 수 있습니다. 크기는 같죠
또한 로테이션은 회전이기 때문에 다른 도메인에서도 회전이 똑같이 일어납니다.
이 특성을 알면 f(x,y)에서 translation을 하거나 rotation을 했을 때 우리는 F(u,v) 모양을 예측 할 수 있습니다.
translation을 했을 때는 크기가 변하지 않고 위상만 변했기 때문에 translation을 하기 전 F(u,v)와 모양이 똑같이 나올 것입니다.
반면 rotation은 회전한 만큼 회전하여 나올 것입니다.
Centering
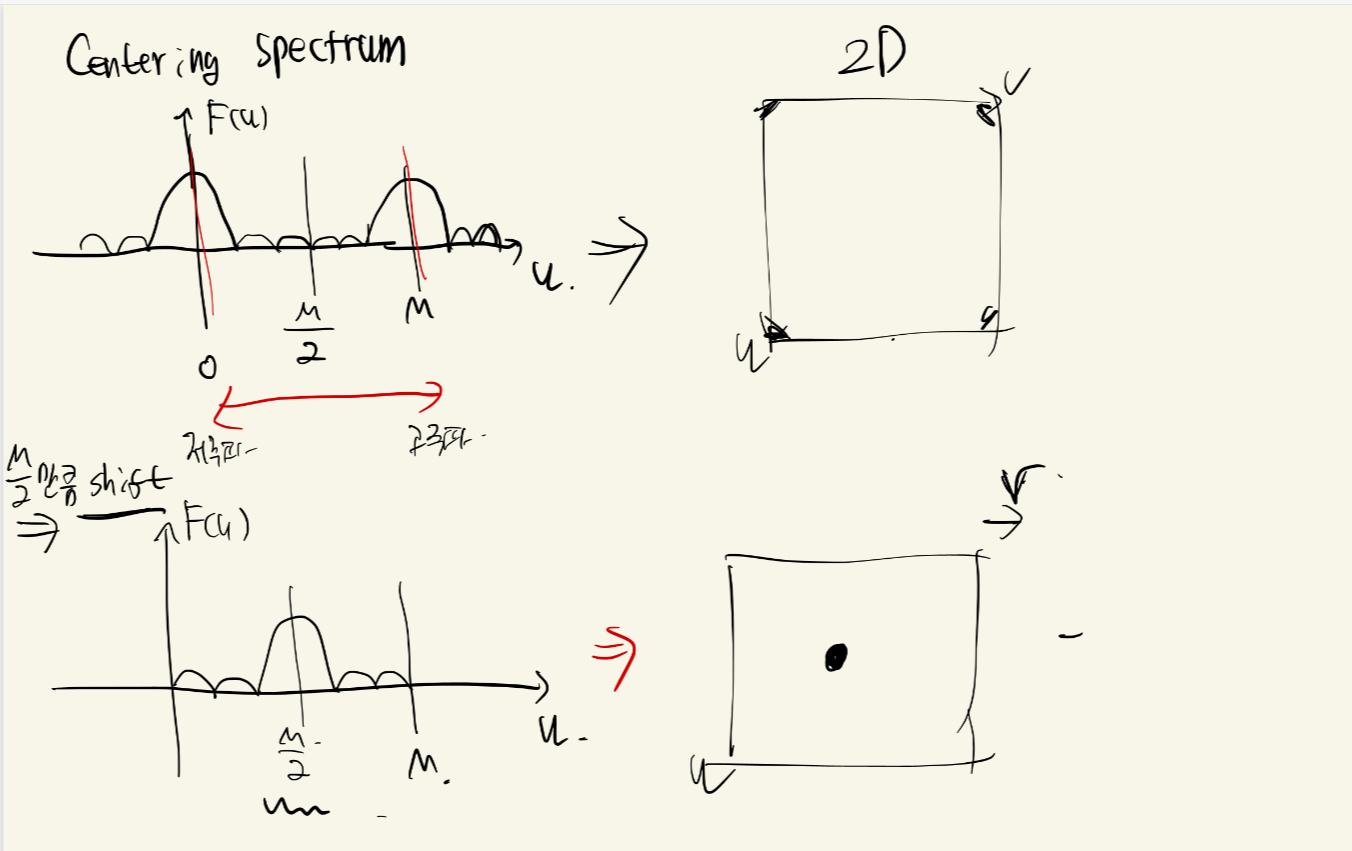
센터링이라는 것은 말 그대로 중앙으로 옮기는 것을 말합니다.
자 우리가 0에서 M까지 뽑아서 본다면 주파수가 0쪽에 몰려있고 M쪽에 몰려있습니다.
이러면 2D에서 주파수를 볼 때 그림과 같이 모서리에서 몰려있게 됩니다.
이렇게 되면 필터를 적용하거나 주파수의 특성을 볼 때 어렵게 되겠죠?
그래서 이것을 중앙으로 예쁘게 옮겨주면 필터링을 하거나 어떤 특성을 볼 때 쉽게 파악 할 수 있습니다.
그래서 주파수를 M/2만큼 쉬프트 해주면 딱 중앙에 주파수들이 모이게 됩니다.

그래서 계산을 직접해보면 저렇게 됩니다. 주파수 도메인에서 M/2, N/2 씩 쉬프트를 시키면 저렇게 Circular의 특성이 적용 되어서 모서리에 있던 것들이 중앙에 모이게 됩니다.
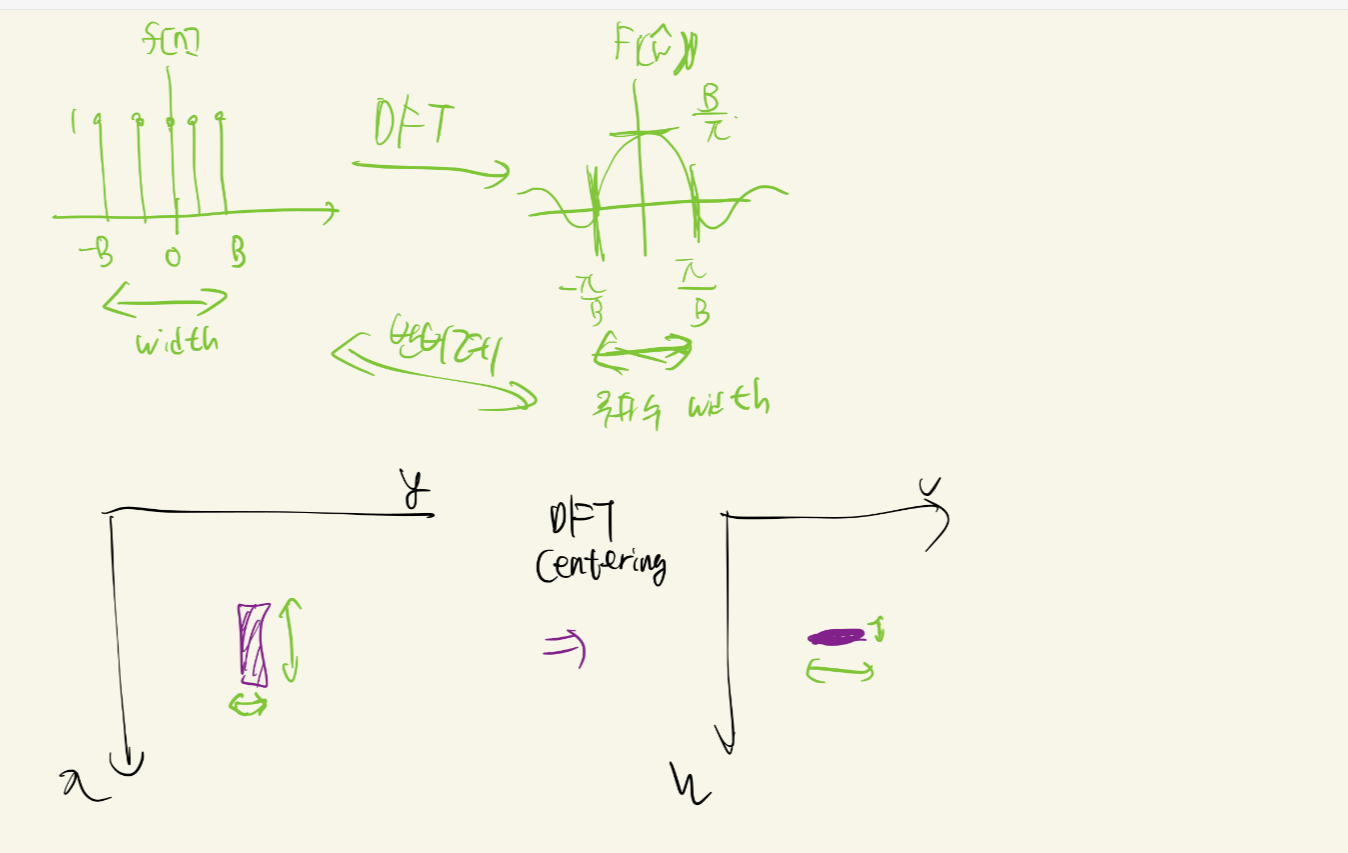
어떤 신호를 DFT를 하고 centering을 한다면 저렇게 보일것입니다. 확대를 하면 sinc function들이 있을 것입니다.
이미지에서의 width와 주파수에서의 width는 반비례 되는 것을 볼 수 있습니다.