힙은 우선순위 큐를 위해 만들어진 자료구조임.
우선순위큐란 완전이진트리인데 부모가 가지는 값은 자식보다 무조건 큰 값을 가지고 있음.( 혹은 무조건 작은 값).
큰 값을 가지는 것을 최대 힙, 작은 값을 가지는 것을 최소 힙이라고 함.
그래서 루트에는 항상 제일 큰 값 혹은 제일 작은 값을 가지고 있는 것이 특징입니다.
기본적으로 구현 같은 경우 배열을 사용하거나 linked를 사용할 수 있습니다.
저는 배열을 사용하여 구현했습니다.
인덱스
루트 노드의 인덱스를 1로 시작하게 하면 (0번 노드는 버림)
부모 인덱스 = (자식 인덱스) / 2
왼쪽 자식 인덱스 = (부모 인덱스) * 2
오른쪽 자식 인덱스 = (부모 인덱스) * 2
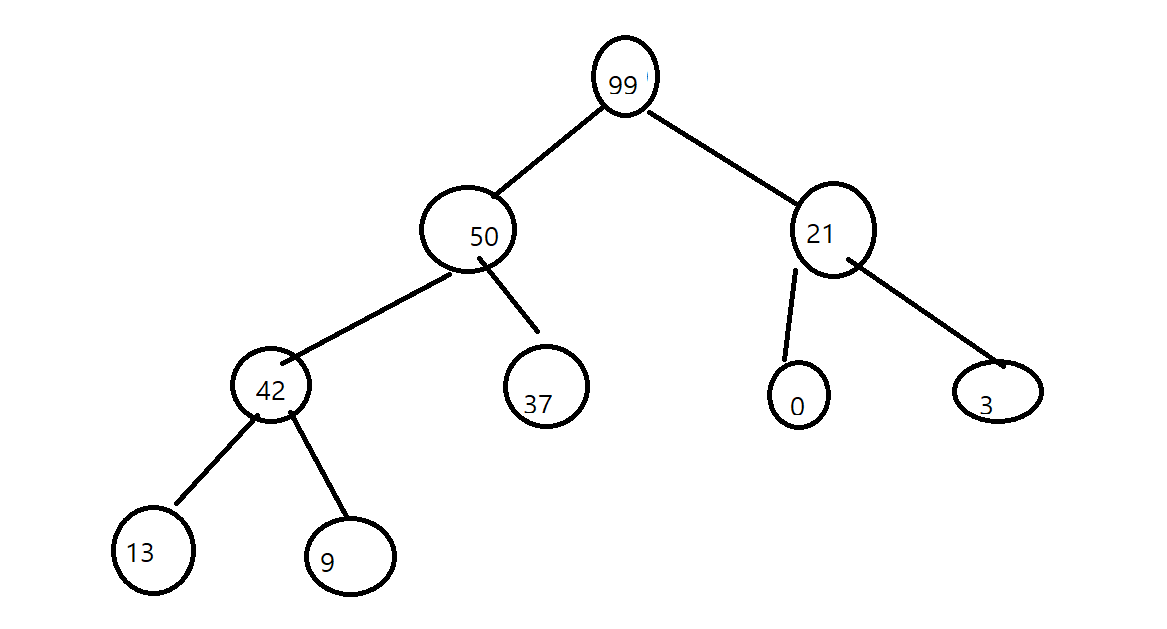
이렇게 나타 낼 수 있겠죠. 위 그림에서 99는 인덱스 1, 50은 2, 21은 3 .....이 될 것입니다.
이러한 트리 구조를 만들기 위해서는 삽입과 삭제 부분이 중요합니다.
삽입
배열의 맨 마지막에 데이터를 삽입하고, 힙 구조를 계속 유지하도록 부모와 값을 바꾸면서 올라가는 방법을 사용합니다.
이 방법을 bubble up이라고 부르고 있습니다.
예를 들어 위 그림에서 80이 들어가면 37의 왼쪽 노드로 들어가게 됩니다.
그 후 부모(37) 과 비교하면 80이 더 크기 때문에 37과 바꿉니다. 그 후 50과 다시 비교하여 바꾸어주고 99와 비교했을 때 더 작기 때문에 종료 됩니다.
삭제
삭제 같은 경우 루트(부모)를 제거합니다.
제거 후 트리를 유지하기 위해 제거 할 때 우리는 마지막의 원소를 루트노드로 가져옵니다.
그 후 자신 보다 더 큰 자식 값과 바꾸며 내려갑니다.
예를 들어 위 그림에서 삭제 연산을 하게 되면 99와 9 가 바뀔 것이고(배열의 크기를 -1 하여 99는 삭제)
9는 50과 21 보다 작고 그 중 50이 더 크기 때문에 50과 바뀌게 됩니다. 그 다음 42, 37 과 비교 하여 42와 바뀌게 되고
그 다음 13과 바뀌고 연산이 종료 됩니다.
시간 복잡도
완전 이진트리는 높이가 O(logN).
삽입과 삭제 모두 최악의 경우에 루트부터 리프까지의 값을 모두 비교하기 때문에 시간복잡도는
O(트리의 높이) = O(logN)이 된다.
Library
C++에 queue에 heap을 응용한 priority_queue가 있음.
기본적으로 최대 힙으로 적용 되어있음.
우선순위 큐에 대한 간단 사용법 -> https://hagisilecoding.tistory.com/60
응용 문제(Library 쓰지 않고 구현)
유저의 id와 재산이 주어질 때 우선순위가 높은 10명을 뽑아내는 문제.
* 재산이 클수록 우선순위가 높으며 재산이 동일한 경우 id가 작은 user가 우선순위가 높음.
* id는 순차적으로 증가하며 주어짐.
전체 코드는 github에 업로드
'CS > 자료구조(Data Structure)' 카테고리의 다른 글
| [자료구조] Trie (트라이) c++ 구현, 설명 (0) | 2023.02.28 |
|---|---|
| [자료구조] Segment Tree(세그먼트 트리) c++ 구현, 설명 (0) | 2023.02.26 |
| [자료구조] Binary Search Tree c++ 구현 [컴공과고씨] (0) | 2023.01.26 |
| [자료구조] Quick sort(퀵 정렬) 구현 c++ [컴공과고씨] (0) | 2023.01.20 |
| [자료구조] Linked List(링크드 리스트) c++ 구현 [컴공과고씨] (0) | 2023.01.19 |