본격적으로 머신러닝을 공부하기 앞서 머신러닝에 필요한 선형대수에 대해서 먼저 간단히 공부하고 머신러닝에 대해서 공부해 보겠습니다.

벡터를 기본적으로 표현하는 방법입니다.
x 밑에 - 를 적어주면 기본적으로 벡터라는 뜻인데 생략하기도 합니다.
열과 행을 모으면 행렬이 되는데 이 행렬은 두 가지로 나타낼 수 있는 모습을 볼 수 있습니다.
하나는 열벡터들의 모음 다른 하는 행 벡터들의 모음 이런식으로 표현할 수 있습니다.
Dot product & Outer product
이제 내적과 외적에 대해서 간단히 보겠습니다.
먼저 내적, inner product or dot product라고 합니다.
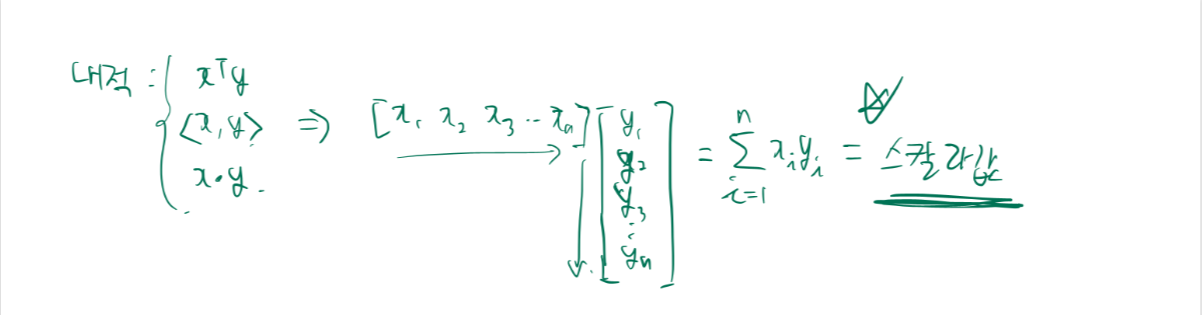
보시면 내적을 표현하는 방법은 3가지가 있습니다. 기본적으로 x 벡터라고 하면 행벡터를 나타내기 때문에 트랜스포스(T)를 취해주어서 열 벡터로 바꾸어 줍니다. 그 다음 y 벡터를 곱해주면 각 인덱스의 x의 요소와 y의 요소가 곱해진 값을 더해주는 것이 내적입니다. 즉, 내적의 값은 스칼라 값입니다.
또한 x와 y를 바꾸어도 성립합니다. -> 교환 법칙 성립.
외적.

외적 같은 경우 일단 중요한 것은 결과 값이 행렬입니다. 또한 교환법칙도 성립하지 않습니다.
한번 보시면 바로 이해가 되실 겁니다.
행렬과 벡터의 곱셈
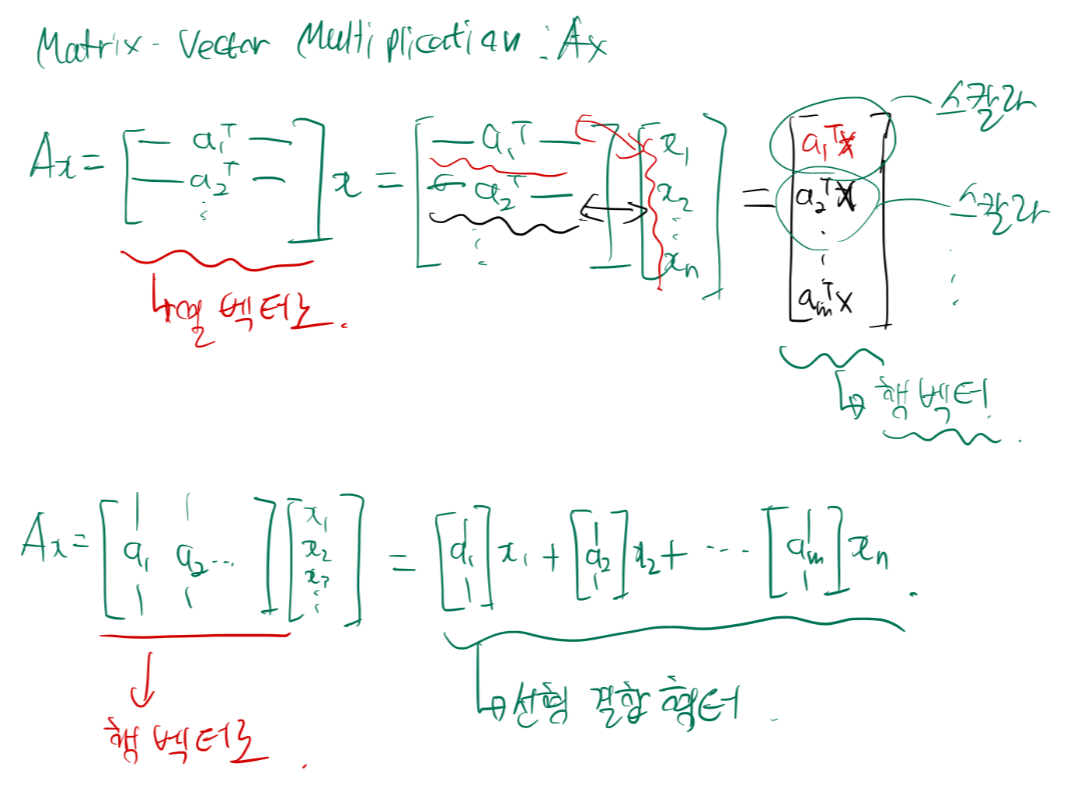

이 특징은 굉장히 중요합니다.
직접 해보신다면 직관적으로 어떤 형태의 결과가 나오는지 보입니다.
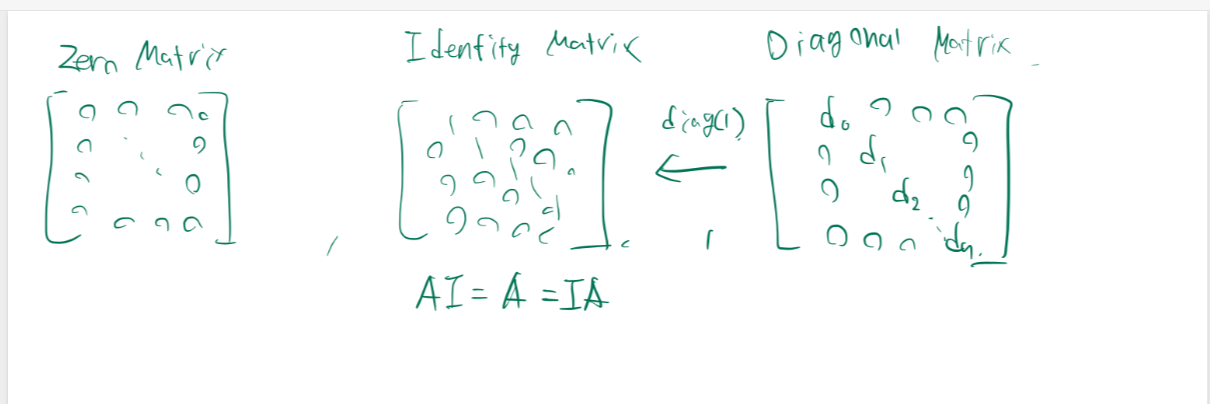
Diagonal Matrix와 행렬의 곱의 특징입니다.
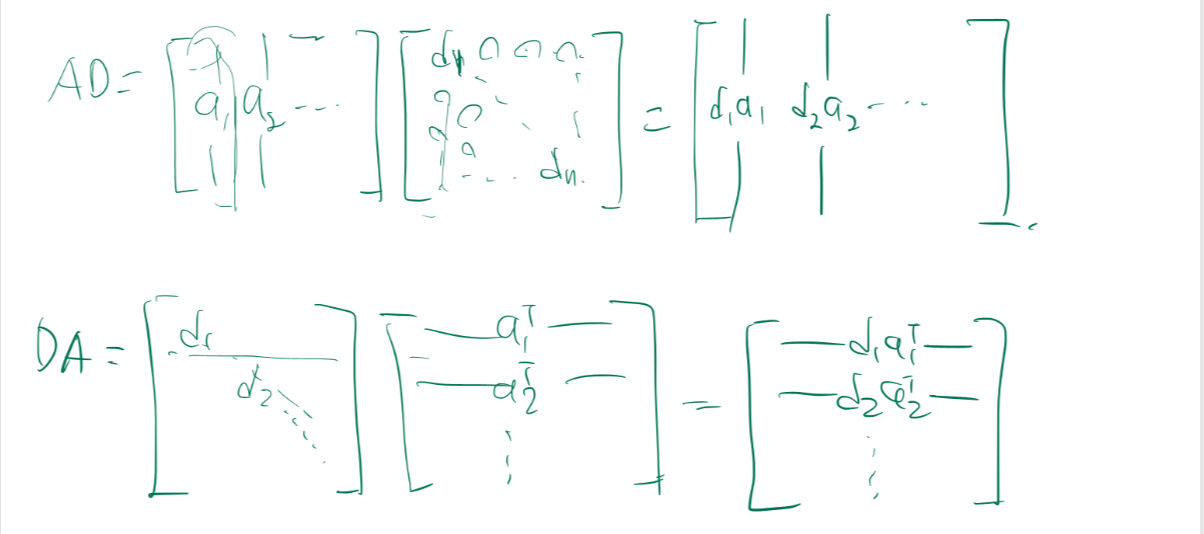
Transpose

대각 행렬을 기준으로 바꾸어 주면되는데 만약 정사각 행렬이 아니면 열과 행의 인덱스를 바꾸어주면 됩니다.
Symmetric Matrix
A행렬에 트랜스포스를 취했을 때 값이 같으면 그 것을 시메트릭 매트릭스라고 합니다.
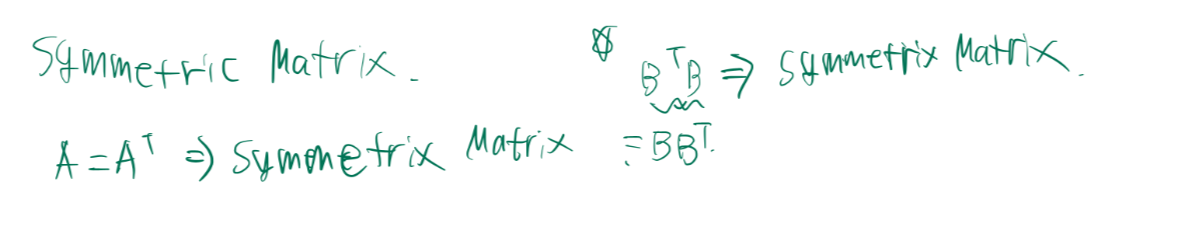
중요한 것은 어떤 행렬의 자기 자신의 프랜스포스를 곱해주면 시메트릭 매트릭스가 나오게 됩니다.
이것도 직접 구해보시면 쉽게 알 수 있습니다.
Trace
대각 성분의 합을 Trace라고 합니다.
tr(AB) = tr(BA) 특징을 가집니다. 기본적으로 행렬은 교환법칙이 성립하지 않는데 trace를 취해주면 성립하게 됩니다.
Linear Independence
어떤 벡터들의 집합이 있을 때 어느 한 벡터를 집합 안에있는 벡터를 스칼라배하여 만들 수 있다면 그것은 종속이고 만약 어느 한 벡터도 만들 수 없다면 독립한다고 한다.
Span
스펜이라는 것은 어떤 벡터 집합에서 벡터를 가지고 만들 수 있는 모든 조합을 말합니다.

이때 벡터들은 선형 독립해야합니다.
Linear Transform
선형 변환이라는 것은 벡터에 행렬을 곱해준 것입니다.

Range & Null Space
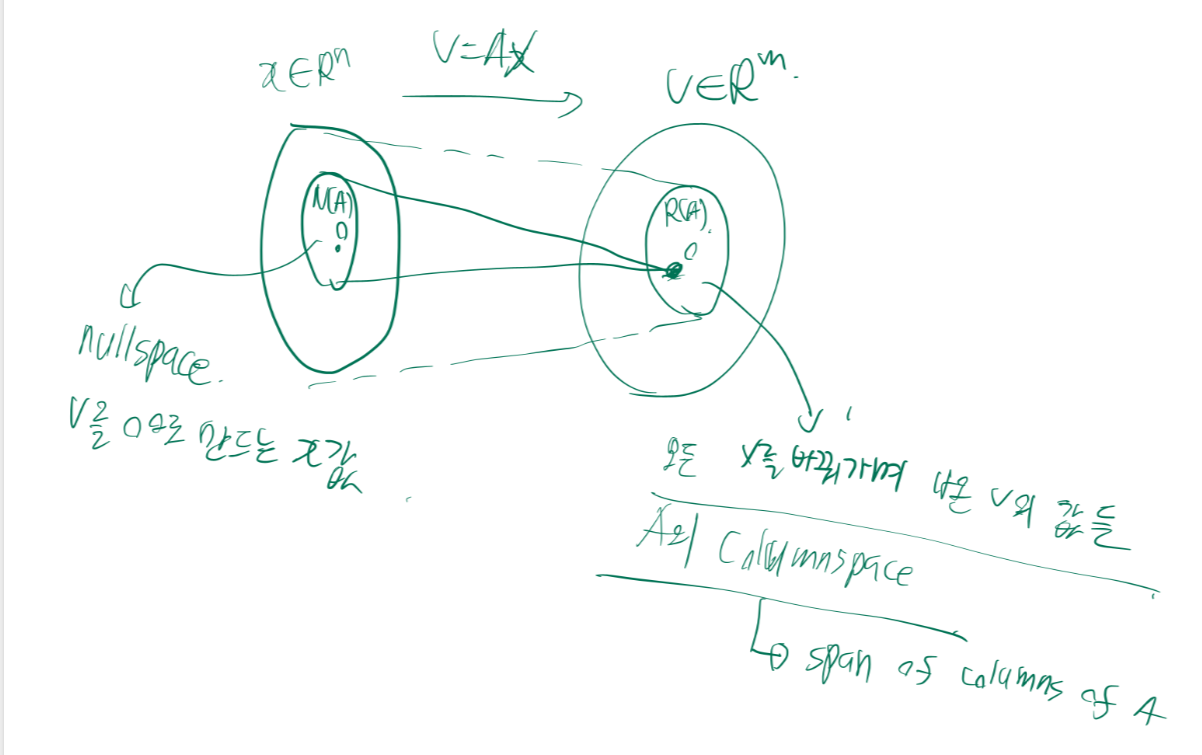
Range는 A의 컬럼 스페이스로 모든 x를 바꿔가며 A를 곱했을 때 나온 v를 모아놓은 것입니다.
Nullspace는 A에 x를 곱했을 때 0이 되게하는 x를 말합니다.
Rank
랭크는 컬럼 랭크와 로우 랭크가 있는데 (column rank, row rank) 컬럼 랭크는 컬럼 선형독립의 개수를 말하고 로우 랭크는 로우 선형독립의 개수를 말합니다.
예를 들어서

이런 행렬이 있다고 하면 1행과 2행은 독립이지만 3행은 1행과 2행을 빼서 만들 수 있기 때문에 위 행렬은 rank가 2이다.
랭크는 칼럼 랭크와 열 랭크는 항상 같습니다. 그렇기 때문에 그냥 rank of A라 하면 행 랭크 or 열 랭크 아무거나 구하셔도 됩니다.
rank(A) <= min(m,n) 이 때 rank(A) = min(m,n) 이면 full rank라고 합니다.
Inverse
역행렬은
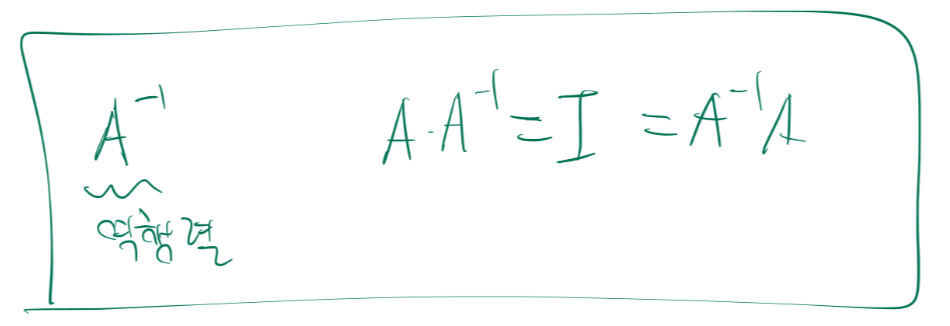
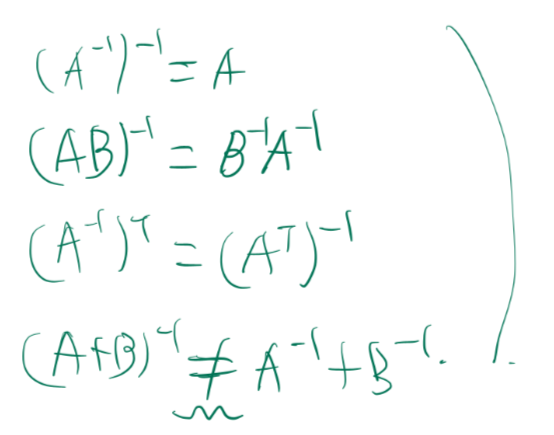
이런 특성을 가지고 있습니다.
역행렬을 가지고 있으면 non - singular 라고 하고 역행렬을 가지지 않으면 singular 라고 합니다.
하지만 역행렬을 직접 구하는 방식은 O(n^3) 시간 복잡도를 가져 컴퓨팅할 때 실제로 잘 사용하지 않습니다.
'CS > 머신러닝' 카테고리의 다른 글
| [머신러닝] 머신러닝을 위한 선형대수(3) Determinant & Decomposition & Quardratic Forms (0) | 2022.07.05 |
|---|---|
| [머신러닝] 머신러닝 선형대수(2) - norm & orthogonality & projection (0) | 2022.07.03 |
| [머신러닝] AI(인공지능)와 ML(머신러닝) (0) | 2022.07.02 |
| [머신러닝] 머신러닝이란 무엇일까? [컴공과고씨] (0) | 2022.07.02 |